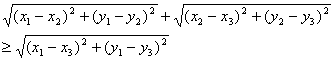2011普通高校招生新课标全国统考大纲：文数

　　（6）会利用丹迪林（Dandelin）双球（如图所示，这两个球位于圆锥的内部，一个位于平面π的上方，一个位于平面的下方，并且与平面π及圆锥面均相切，其切点分别为F、E）证明上述定理①情形：当β>α时，平面π与圆锥的交线为椭圆.（图中上、下两球与圆锥面相切的切点分别为点B和点C，线段BC与平面π相交于点A.）

　　（7）会证明以下结果：

　　①在（6）中，一个丹迪林球与圆锥面的交线为一个圆，并与圆锥的底面平行，记这个圆所在平面为π'；

　　②如果平面π与平面π'的交线为m，在（5）①中椭圆上任取一点A，该丹迪林球与平面π的切点为F，则点A到点F的距离与点A到直线m的距离比是小于1的常数e.（称点F为这个椭圆的焦点，直线m为椭圆的准线，常数e为离心率.）

　　（8）了解定理（5）③中的证明，了解当无限接近时,平面π的极限结果.

　　2.坐标系与参数方程

　　（1）坐标系

　　① 理解坐标系的作用.

　　② 了解在平面直角坐标系伸缩变换作用下平面图形的变化情况.

　　③ 能在极坐标系中用极坐标表示点的位置，理解在极坐标系和平面直角坐标系中表示点的位置的区别，能进行极坐标和直角坐标的互化.

　　④ 能在极坐标系中给出简单图形（如过极点的直线、过极点或圆心在极点的圆）的方程.通过比较这些图形在极坐标系和平面直角坐标系中的方程，理解用方程表示平面图形时选择适当坐标系的意义.

　　⑤ 了解柱坐标系、球坐标系中表示空间中点的位置的方法，并与空间直角坐标系中表示点的位置的方法相比较，了解它们的区别.

　　（2）参数方程

　　① 了解参数方程，了解参数的意义.

　　② 能选择适当的参数写出直线、圆和圆锥曲线的参数方程.

　　③ 了解平摆线、渐开线的生成过程，并能推导出它们的参数方程.

　　④ 了解其他摆线的生成过程，了解摆线在实际中的应用，了解摆线在表示行星运动轨道中的作用.

　　3．不等式选讲

　　（1）理解绝对值的几何意义，并能利用含绝对值不等式的几何意义证明以下不等式：

　　①|a+b|≤|a|+|b|

　　②|a-b|≤|a-c|+|c-b|

　　③会利用绝对值的几何意义求解以下类型的不等式：

　　|ax+b|≤c；|ax+b|≥c；|x-a|+|x-b|≥c.

　　（2）了解下列柯西不等式的几种不同形式，理解它们的几何意义，并会证明.

　　①柯西不等式的向量形式：|α||β|≥|αβ|

　　②(a2+b2)(c2+d2)≥(ac+bd)2

　　③

（通常称为平面三角不等式）

　　（3）会用参数配方法讨论柯西不等式的一般情形：

　　（4）会用向量递归方法讨论排序不等式

　　（5）了解数学归纳法的原理及其使用范围，会用数学归纳法证明一些简单问题

　　（6）会用数学归纳法证明贝努利不等式：

　　(1+x)n>1+nx (x>-1,x≠0,n为大于1的正整数)，了解当n为大于1的实数时贝努利不等式也成立

　　（7）会用上述不等式证明一些简单问题。能够利用平均值不等式、柯西不等式求一些特定函数的极值

　　（8）了解证明不等式的基本方法；比较法、综合法、分析法、反证法、放缩法