2011普通高校招生新课标全国统考大纲：文数

　　（1）和与差的三角函数公式

　　① 会用向量的数量积推导出两角差的余弦公式.

　　② 能利用两角差的余弦公式导出两角差的正弦、正切公式.

　　③ 能利用两角差的余弦公式导出两角和的正弦、余弦、正切公式，导出二倍角的正弦、余弦、正切公式，了解它们的内在联系.

　　（2）简单的三角恒等变换

　　能运用上述公式进行简单的恒等变换（包括导出积化和差、和差化积、半角公式，但对这三组公式不要求记忆）.

11．解三角形

　　（1）正弦定理和余弦定理

　　掌握正弦定理、余弦定理，并能解决一些简单的三角形度量问题.

　　(2) 应用

　　能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题.

　　12．数列

　　（1）数列的概念和简单表示法

　　①了解数列的概念和几种简单的表示方法（列表、图像、通项公式）.

　　②了解数列是自变量为正整数的一类函数.

　　（2）等差数列、等比数列

　　① 理解等差数列、等比数列的概念.

　　② 掌握等差数列、等比数列的通项公式与前n项和公式.

　　③ 能在具体的问题情境中，识别数列的等差关系或等比关系，并能用有关知识解决相应的问题.

　　④ 了解等差数列与一次函数、等比数列与指数函数的关系.

　　13．不等式

　　（1）不等关系

　　了解现实世界和日常生活中的不等关系，了解不等式（组）的实际背景.

　　（2）一元二次不等式

　　① 会从实际情境中抽象出一元二次不等式模型.

　　② 通过函数图像了解一元二次不等式与相应的二次函数、一元二次方程的联系.

　　③ 会解一元二次不等式，对给定的一元二次不等式，会设计求解的程序框图.

　　（3）二元一次不等式组与简单线性规划问题

　　① 会从实际情境中抽象出二元一次不等式组.

　　② 了解二元一次不等式的几何意义，能用平面区域表示二元一次不等式组.

　　③ 会从实际情境中抽象出一些简单的二元线性规划问题，并能加以解决.

　　① 了解基本不等式的证明过程.

　　② 会用基本不等式解决简单的最大（小）值问题.

　　14．常用逻辑用语

　　（1）命题及其关系

　　① 理解命题的概念.

　　②了解“若p，则q”形式的命题的逆命题、否命题与逆否命题，会分析四种命题的相互关系.

　　③ 理解必要条件、充分条件与充要条件的意义.

　　（2）简单的逻辑联结词

　　了解逻辑联结词“或”、“且”、“非”的含义.

　　（3）全称量词与存在量词

　　① 理解全称量词与存在量词的意义.

　　② 能正确地对含有一个量词的命题进行否定.

　　15．圆锥曲线与方程

　　圆锥曲线与方程

　　① 了解圆锥曲线的实际背景，了解圆锥曲线在刻画现实世界和解决实际问题中的作用.

　　② 掌握椭圆的定义、几何图形、标准方程及简单几何性质.

　　③ 了解双曲线、抛物线的定义、几何图形和标准方程，知道它们的简单几何性质.

　　④ 理解数形结合的思想.

　　⑤ 了解圆锥曲线的简单应用.

　16．导数及其应用

　　（1）导数概念及其几何意义

　　① 了解导数概念的实际背景.

　　② 理解导数的几何意义.

　　（2）导数的运算

　　② 能利用下面给出的基本初等函数的导数公式和导数的四则运算法则求简单函数的导数.

　　常见基本初等函数的导数公式：

　　.（a>0,且a≠1）

　　常用的导数运算法则：

　　法则2.

　　法则3 .

　　（3）导数在研究函数中的应用

　　① 了解函数单调性和导数的关系；能利用导数研究函数的单调性，会求函数的单调区间（其中多项式函数一般不超过三次）.

　　② 了解函数在某点取得极值的必要条件和充分条件；会用导数求函数的极大值、极小值（其中多项式函数一般不超过三次）；会求闭区间上函数的最大值、最小值（其中多项式函数一般不超过三次）.

　　（4）生活中的优化问题.

　　会利用导数解决某些实际问题.

　　17．统计案例

　　了解下列一些常见的统计方法，并能应用这些方法解决一些实际问题.

　　(1)独立性检验

　　了解独立性检验（只要求2×2列联表）的基本思想、方法及其简单应用.

　　(2) 回归分析

　　了解回归分析的基本思想、方法及其简单应用.

　　18．推理与证明

　　（1）合情推理与演绎推理

　　① 了解合情推理的含义，能利用归纳和类比等进行简单的推理，了解合情推理在数学发现中的作用.

　　② 了解演绎推理的重要性，掌握演绎推理的基本模式，并能运用它们进行一些简单推理.

　　③ 了解合情推理和演绎推理之间的联系和差异.

　　（2）直接证明与间接证明

　　① 了解直接证明的两种基本方法：分析法和综合法；了解分析法和综合法的思考过程、特点.

　　② 了解间接证明的一种基本方法──反证法；了解反证法的思考过程、特点.

　　19．数系的扩充与复数的引入

　　（1）复数的概念

　　①理解复数的基本概念.

　　②理解复数相等的充要条件.

　　③ 了解复数的代数表示法及其几何意义.

　　（2）复数的四则运算

　　①会进行复数代数形式的四则运算.

　　②了解复数代数形式的加、减运算的几何意义.

　　20．框图

　　（1）流程图

　　① 了解程序框图.

　　② 了解工序流程图（即统筹图）.

　　③ 能绘制简单实际问题的流程图，了解流程图在解决实际问题中的作用.

　　（2）结构图

　　①了解结构图.

　　②会运用结构图梳理已学过的知识、整理收集到的资料信息.

（二）选考内容与要求

　　1．几何证明选讲

　　（1）了解平行线截割定理，会证直角三角形射影定理.

　　（2）会证明并应用圆周角定理、圆的切线的判定定理及性质定理.

　　（3）会证明并应用相交弦定理、圆内接四边形的性质定理与判定定理、切割线定理.

　　（4）了解平行投影的含义，通过圆柱与平面的位置关系，了解平行投影；会证平面与圆柱面的截线是椭圆（特殊情形是圆）.

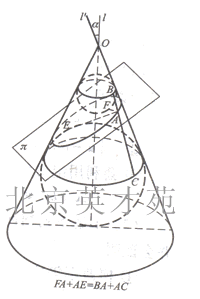
（5）了解下面定理：

　　定理在空间中，取直线为轴，直线与相交于点，其夹角为围绕旋转得到以为顶点，为母线的圆锥面，任取平面π，若它与轴交角为（π与平行，记=0），则：

　　①>，平面π与圆锥的交线为椭圆；

　　②=，平面π与圆锥的交线为抛物线；

　　③<，